728x90
1. 수식 트리
: 후위 순회를 사용
- 루트 노드보다 자식 노드를 먼저 방문하여 수식의 값을 계산
- 연산자와 피연산자로 구성
- 연산자(operator) : 비단말노드
- 피연산자(operand) : 단말노드

계산 순서는 다음과 같다.
32*56*+
==> 36
#include <stdio.h>
typedef struct TreeNode {
int data;
struct TreeNode* left, * right;
} TreeNode;
// +
// * +
// 1 4 16 25
TreeNode n1 = { 1, NULL, NULL };
TreeNode n2 = { 4, NULL, NULL };
TreeNode n3 = { '*', &n1, &n2 };
TreeNode n4 = { 16, NULL, NULL };
TreeNode n5 = { 25, NULL, NULL };
TreeNode n6 = { '+', &n4, &n5 };
TreeNode n7 = { '+', &n3, &n6 };
TreeNode* exp = &n7;
// 수식 계산 함수
int evaluate(TreeNode* root)
{
if (root == NULL) {
return 0;
}
if (root->left == NULL && root->right == NULL) {
return root->data;
}else {
int op1 = evaluate(root->left);
int op2 = evaluate(root->right);
printf("중간 %d %c %d을 계산합니다.\n", op1, root->data, op2);
switch (root->data) {
case '+': return op1 + op2;
case '-': return op1 - op2;
case '*': return op1 * op2;
case '/': return op1 / op2;
}
}
return 0;
}
//
int main(void)
{
printf("최종 수식의 계산 결과 값 : %d \n", evaluate(exp));
return 0;
}
실행결과
중간 1 * 4을 계산합니다.
중간 16 + 25을 계산합니다.
중간 4 + 41을 계산합니다.
최종 수식의 계산 결과 값 : 45
2. 이진 탐색 트리(Binary search tree)
: 이진트리 기반의 탐색 작업을 효율적으로 하기 위한 자료구조
이진 탐색 트리의 정의
- 모든 원소의 키는 유일한 키를 가진다.
- 왼쪽 서브 트리 키들은 루트 키보다 작다.
- 오른쪽 서브 트리의 키들은 루트 키보다 크다. : key(왼쪽서브트리) <= key(루트노드) <= key(오른쪽서브트리)
- 왼쪽과 오른쪽 서브 트리도 이진 탐색 트리이다.

이진 탐색을 중위 순회하면 오름차순으로 정렬된 값을 얻을 수 있음
3 - 7 - 12 - 18 - 26 - 27 - 31
주어진 탐색 키 값과 루트 노드의 키 값의 비교에 따라 분류
- 비교한 결과가 같으면 성공적으로 종료
- 비교한 결과가 주어진 키 값이 루트 노드의 키 값보다 작으면 탐색은 해당 루트 노드의 왼쪽 자식 노드를 기준으로 다시 비교를 시작
- 비교한 결과가 주어진 키 값이 루트 노드의 키 값보다 크면 탐색은 해당 루트 노드의 오른쪽 자식 노드를 기준으로 다시 비교를 시작
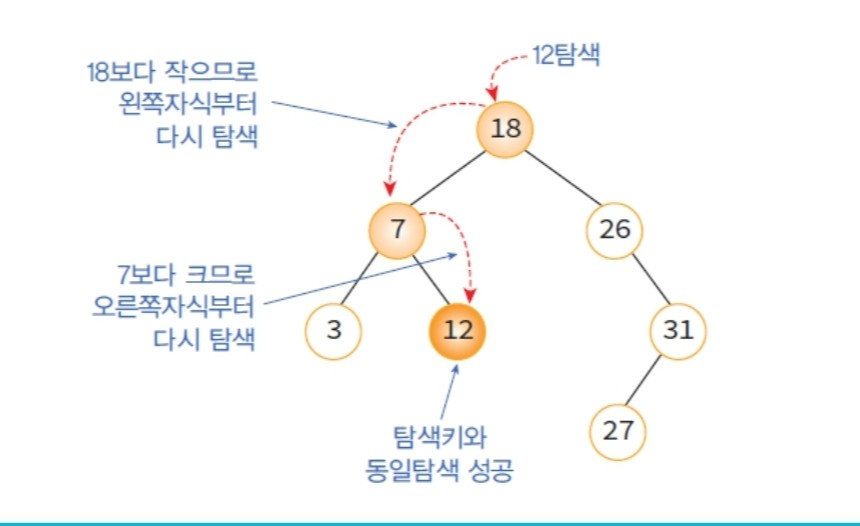
이진 탐색 트리(순환적)
TreeNode* search(TreeNode* node, int key) {
if (node == NULL) return NULL;
if (key == node->key) return NULL;
else if (key < node->key)
return search(node->left, key);
else
return search(node->right, key);
}
이진 탐색 트리(반복적)
TreeNode* search(TreeNode* node, int key) {
while (node != NULL) {
if (key == node->key) return node;
else if (key < node->key)
node = node->left;
else
node = node->right;
}
return NULL;
}
2-1. 삽입연산
원소를 삽입하기 위해서는 먼저 탐색을 수행이 필요
- 동일한 키 값을 갖은 원소가 없어야 하기 때문
- 탐색에 실패한 위치가 바로 새로운 노드를 삽입하는 위치가 되므로

이진트리 삽입 프로그램
TreeNode* insert_node(TreeNode* node, int key) {
if (node == NULL) return new_node(key);
if (key < node->key)
node->left = inset_node(node->left, key);
else if (key > node->key)
node->right = insert_node(node->right, key);
return node;
}
TreeNode* new_node(int item) {
TreeNode* temp = (TreeNode*)malloc(sizeof(TreeNode));
temp->key = item;
temp->left = temp->right = NULL;
return temp;
}
2-2. 삭제연산
삭제 시 고려해야 하는 3가지 경우
1) 삭제하려는 노드가 단말 노드인 경우
2) 삭제하려는 노드가 하나의 왼쪽이나 오른쪽 서브 트리 중 하나만 가지고 있는 경우
3) 삭제하려는 노드가 두 개의 서브 트리 모두 가지고 있는 경우
ex) case 1: 삭제하려는 노드가 단말 노드인 경우
- 단말 노드의 부모 노드를 찾아서 연결을 끊음

ex) case 2: 삭제하려는 노드가 하나의 서브 트리만 갖고 있는 경우
- 삭제되는 노드가 왼쪽이나 오른쪽 서브 트리 중 하나만 갖고 있을 때, 그 노드는 삭제하고 서브 트리는 부모 노드에게 연결

ex) case 3: 삭제하려는 노드가 두 개의 서브 트리를 갖고 있는 경우
- 삭제 노드와 가장 비슷한 값을 가진 노드를 삭제 노드 위치로 가져옴

가장 비슷한 값이란?
: 각 서브트리를 중위 순회하였을 때 노드 순서의 바로 전 노드와 바로 후 노드가 해당 예시에선 노드 18의 직전 노드는 12가 되고 직후 노드는 22가 된다.
2-3. 이진 탐색 트리의 성능 분석
평균적인 시간 복잡도는 O(log2n)
728x90
'[Computer Science] > [자료구조 in C]' 카테고리의 다른 글
| [자료구조] 이진트리와 시간복잡도 로그의 의미 (0) | 2022.06.19 |
|---|---|
| [자료구조] 정렬 : C언어 (0) | 2022.06.18 |
| [자료구조] 트리_상 : C언어 (0) | 2022.06.18 |
| [자료구조] 연결리스트(2) : C언어 (0) | 2022.05.30 |
| [자료구조] 연결리스트(1) : C언어 (0) | 2022.05.23 |
![[자료구조] 트리_하 : C언어](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FqvjLq%2FbtrE4UOdgLm%2FGu5RZI4U43Z6XMgTWlKkvk%2Fimg.png)