데이크스트라 또는 다익스트라 알고리즘이라 불리는 알고리즘을 알아보겠습니다.
다익스트라 알고리즘은 특정 노드에서 다른 노드로의 최단경로를 구하는 알고리즘입니다. 다익스트라 알고리즘에는 그리디와 다이나믹 프로그래밍이 녹아들어 있습니다. 이전 최소거리를 기억한다는 점에서는 다이나믹 프로그래밍이 현재 시점에서 항상 최소값을 찾는다는점이 그리디 알고리즘이 녹아있음을 알 수 있습니다.
다익스트라 알고리즘은 음의 간선이 존재하지 않을때 정상적으로 작동하는 알고리즘입니다. 모든 간선의 값은 0이상이며 그래서 GPS등에 활용할 수 있는 실생활에 적합한 알고리즘입니다.
다익스트라 알고리즘의 과정을 그림으로 알아보겠습니다.

시작 노드 A에서 도착 노드 F까지의 과정을 알아보겠습니다. 간선은 노드간 이동값(거리)입니다.

노드 A에서 갈 수 없는 노드는 무한대(엄청 큰값)으로 표현합니다.
그 다음은 이 거리 중 가장 작은 값을 가진 노드로 이동합니다. 이동 값이 가장 작은 노드는 B이므로 노드B로 이동하겠습니다.

노드 B에서 갈 수 있는 노드는 노드 E이므로 갱신할 수 있는지를 확인해 줍니다. 그리고 A에서 E로 가는 길의 최소거리를 찾았으므로 E로 가는 값을 갱신해 줍니다. 그리고 노드 E는 방문처리를 해줍니다. 값 1은 A에서 B로 가는 최소값을 의미하고 그 최소값에서 B에서 E로 가는 값 2를 더하면 3이 A에서 E로 가는 최소값이 됩니다.
그 다음노드로 이동할때는 수정된 표에서 방문하지 않은 노드 중 가장 작은 값을 가지는 노드로 이동합니다. C노드로 이동하겠습니다.
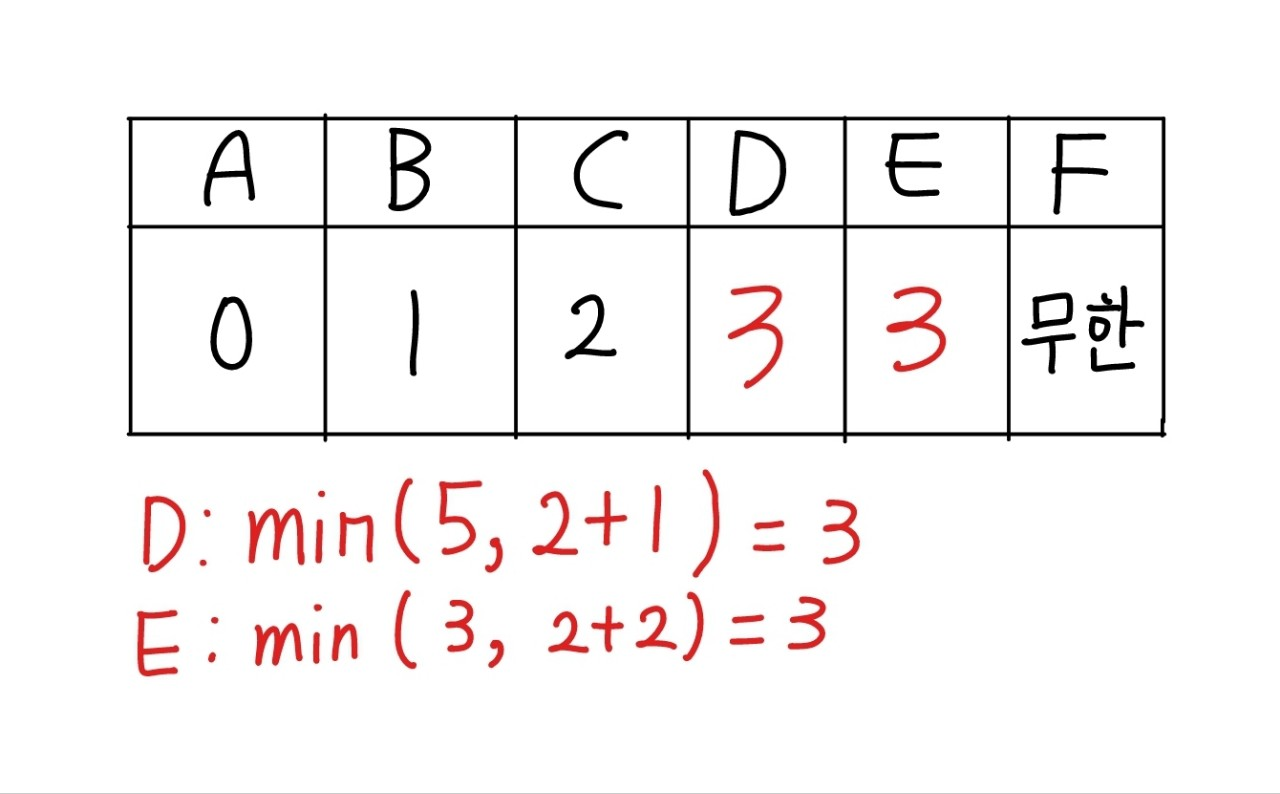
노드 C에서 갈 수 있는 노드는 D와 E입니다. C에서 D로 가는 최소거리를 찾았으므로 갱신해줍니다. 하지만 C에서 E로 가는 거리는 기존의 거리가 더 작으니 갱신하지 않습니다.
다음 가장 작은 노드는 D와 E인인데 최소값이 같은 경우는 노드의 순번이 빠른순서(작은순서) 먼저 탐색합니다. D로 가겠습니다.

노드 D에서 갈 수 있는 노드는 F입니다. F는 무한대와 3+1 두 가지 경우가 있으므로 최소값을 갱신해서 4가 됩니다.
이렇게 도착 노드 F까지의 과정을 끝냈습니다. 노드 E에서 F를 가는 경우도 있지만 다익스트라 알고리즘은 처음 방문할때 최소거리를 보장해줍니다. E에서 F를 가는 경우를 계산해주면 3+2 = 5이므로 갱신되지 않습니다.
목적지가 F였으므로 A -> C -> D -> F가 됩니다.
여기서 생각해볼 점은 한번 방문하면 그 값은 최소값을 보장하고 그 이후는 그 최소값을 이용해서 다른 노드와의 최소값을 갱신해준다는 점입니다.
'[Computer Science] > [알고리즘]' 카테고리의 다른 글
| [Algorithm] BackTracking(백트래킹) 알고리즘 (0) | 2022.07.16 |
|---|---|
| [Algorithm] 다이나믹 프로그래밍(DP) - 탑다운, 바텀업 (0) | 2022.07.14 |
| [Algorithm] 플로이드 워셜 알고리즘 (0) | 2022.07.10 |
| [Algorithm] 0-1 BFS (0) | 2022.07.08 |
| [Algorithm] 에라토스테네스의 체, 소수 판정시 제곱근까지 확인하는 이유(python) (0) | 2022.07.05 |
![[Algorithm] 다익스트라 알고리즘](https://img1.daumcdn.net/thumb/R750x0/?scode=mtistory2&fname=https%3A%2F%2Fblog.kakaocdn.net%2Fdn%2FXnMzJ%2FbtrGSULwAW7%2FvLwq0j5Ahfkzj1u1cSKCFK%2Fimg.png)